Support Vector Machine is a Supervised Learning algorithm.

1. What is Support Vector Machine
2. Types of SVM
3. SVM Terminologies
   • Hyperplane
   • Margin
   • Support Vectors
   • Hyper-parameter
   • Regularization (C)
   • Gamma
   • Kernel
4. Applications of SVM
5. Pros & Cons
6. Conclusion

What is Support Vector Machine (SVM)

                SVM is one of the Supervised Learning Algorithm, used for classification and regression problems. The main objective of SVM is to find the optimal Hyper-plane in N-Dimensional space (N-Features) helping in evidently classifying the data points.

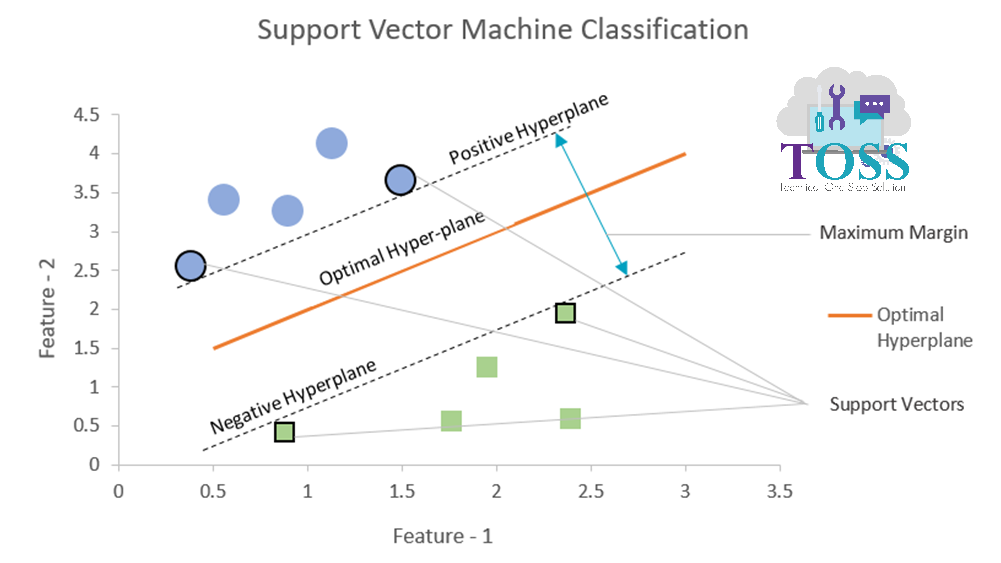
The below Graph represents the Optimal Hyperplane in SVM.

Types of SVM

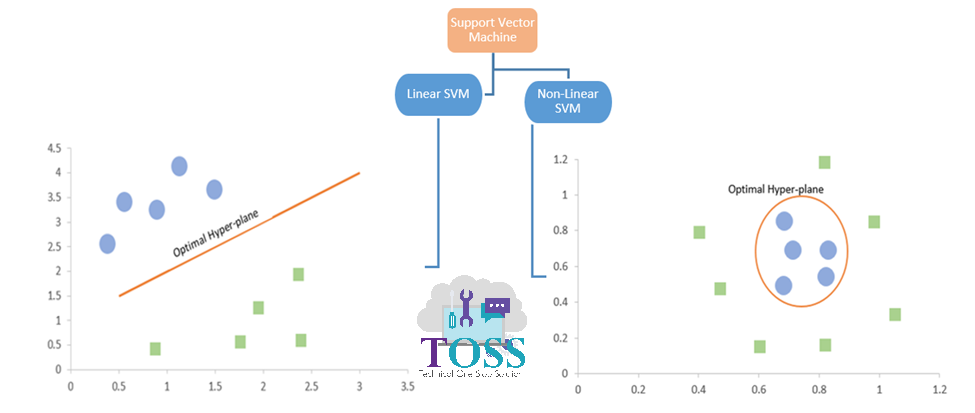
SVM Terminologies

Hyperplanes

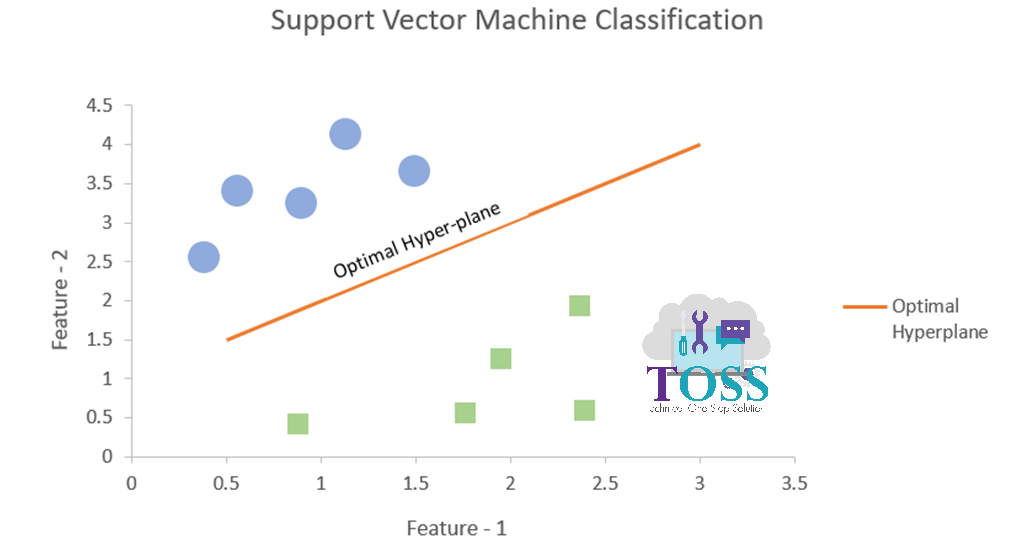
Here there are 2 classes having different shapes and let’s understand on basis of this example.

1. Hyperplane:
2. Hyperplane is the decision boundary that help to classify the data points belonging to respective the classes.
3. Considering the figure ii,

Hyperplane segregates two different classes belonging to circle and square classes respectively.

• If Number of features is 2 then, Hyperplane will be single line (Linear SVM) or Non-Linear SVM.
• If Number of features is 3 then, Hyperplane will be a 2-D Graphical plane.

The below Graph represents Positive, Negative Hyperplanes.

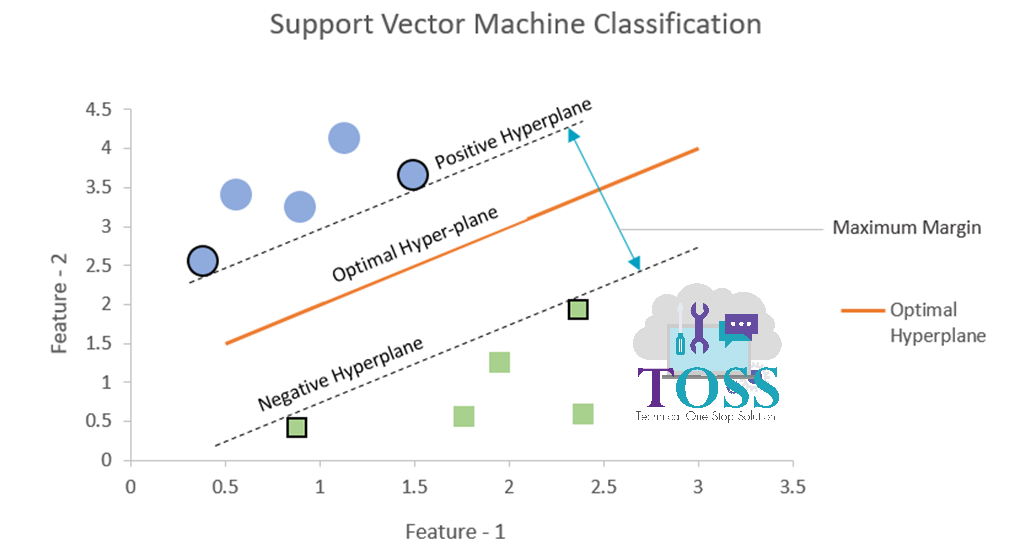
Now Consider figure iii (for point 2, 3)

1. Positive Hyperplane:
2. The data point closest above/right to the optimal hyperplane forms a positive hyperplane.
3. Negative Hyperplane:
4. The data point closest below/left to the optimal hyperplane forms a negative hyperplane.

Margin

1. Margin: The distance between Positive Hyperplane and Negative Hyperplane is said to be a Margin.
2. Maximum Margin: The maximum distance between Positive Hyperplane and Negative Hyperplane is said to be Maximum Margin.

(For visual representation kindly look up figure iv)

The below graphs represents the Small Margin and Large Margin

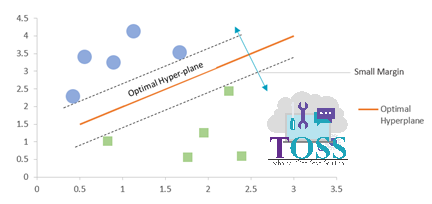
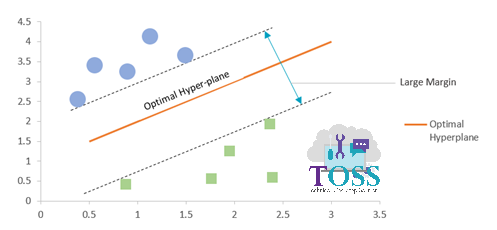
Note: From two of the above Graph,

1. SVM’s motive is to increase or to achieve the Large Margin (Maximum Margin).
2. Larger the Margin, better the accuracy and stability of a model.

Support Vectors

The below Graph shows the representation of Support Vectors.

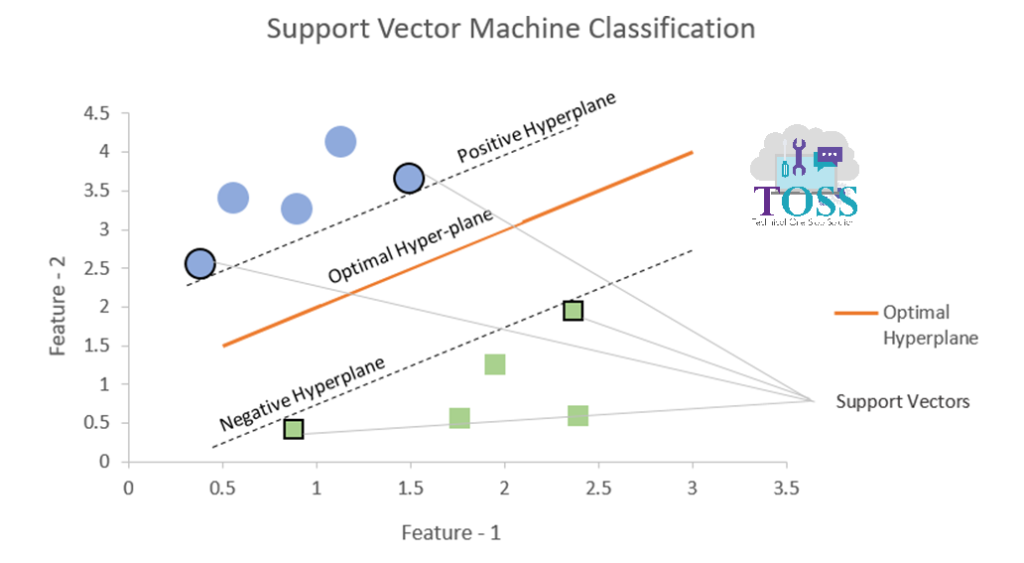
• Support Vectors are the data points help in building SVM.
• The Shapes, in figure vi, outlined black in colour are the Support Vectors data points.

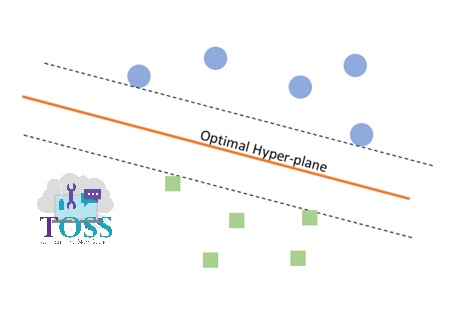
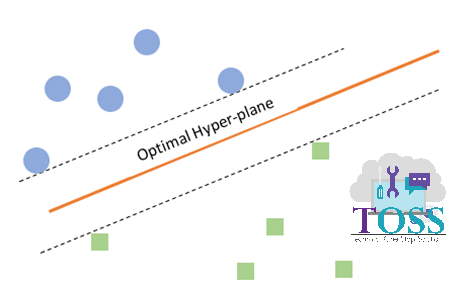
• Consider in figure vii, viii:
  • When compared, we could observe that orientation (angle) of the Hyperplane, is different.
  • The data points supporting to get Hyperplane and Orientation of Hyperplane is done by Support Vectors.

Hyper-parameter

                Hyper-parameter are the parameters whose values control the learning process of a model.

Example:

• Test-train datasets split ratio.
• Activation functions in Neural Network (ReLU, Sigmoid, etc…)

Regularization (C)

                Regularization (C) is a hyper-parameter in SVM for error control or control on misclassifying classes.

• It is used and must be set before training a model.
• Higher the C value lower the error/ less Misclassification.
• Lower the C value higher the error/ high Misclassification.
• C values: 0.001, 0.01, 1, 10, 100

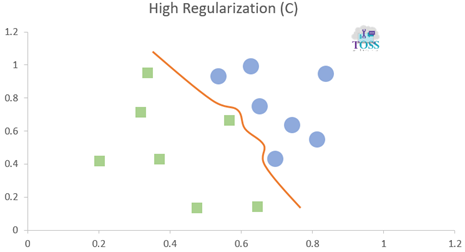
Note:

• Low error means not that the model is best.
• It Completely depends on datasets that how much error it must have to become a better model.
• There is no rule that we need to apply/ work with high, low error.

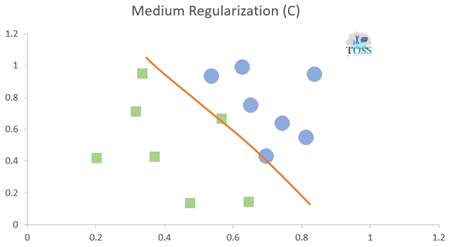
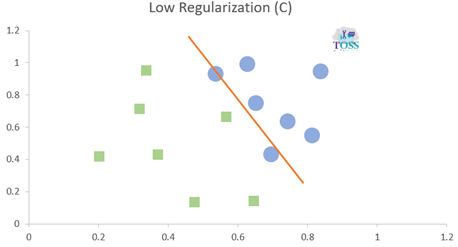
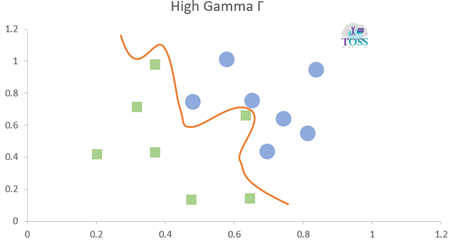
Gamma-Γ

                Gamma is a hyper-parameter which is used to define the curvature.

• If it is used, then need to be defined before training a model.
• Higher the Gamma value more the curvature, more the chance that a model could over-fit.
• Lower the Gamma value less the curvature.
• Gamma values: 0.001, 0.01, 1, 10, 100

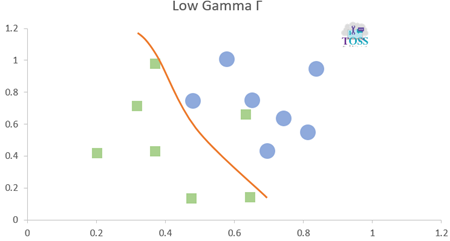
Overview of Regularization and Gamma:

• Regularization (C)
  • It is s a hyper-parameter used in SVM to control error.
  • It must be used before training any model.
  • C values: 0.001, 0.01, 1, 10, 100
• Gamma Γ
  • It is s a hyper-parameter used in SVM to control curvature.
  • It is optional to be used, if used then must be used before training a model.
  • Gamma values: 0.001, 0.01, 1, 10, 100

Have a Question?

• Which hyper-parameter (Regularization/ Gamma) must be used to train a model and to be best?
  • It depends on the requirement and the datasets which you are working in.
  • Some datasets need only Regularization to perform at its best, some datasets might need both Regularization and Gamma.

Kernel (sklearn)

                Kernel is a hyper-parameter in SVM used to perform learning operations based on functionality.

• Kernel functionalities:
  • Linear Kernel
  • Sigmoid Kernel
  • Gaussian Kernel Radial Basis Function
  • Polynomial Kernel
• The functionality will improve/ affect the accuracy depending on datasets.

Applications of SVM?

• Facial Expression classification.
• Speech Recognition.
• Texture classification.
• Image classification.

Pros & Cons

Advantages

• Simple Machine Learning algorithm.
• Significant accuracy with Less power consumption.
• Memory efficient.
• Good accuracy with smaller, cleaner datasets.
• Effective when number of dimensions is greater than number of samples.
• Risk of over-fitting is less.
• Handles non-linear data efficiently

Disadvantages

• In-effective performance for overlapping datasets (having outliers).
• Difficult to understand and interpret.
• Performs poor for larger Datasets.
• Less effective with Noisy Datasets.
• Feature scaling is required.
• SVM is not probabilistic model.
• Choosing Optimal Kernel is a difficult task.

Conclusion

Thus, we conclude the basic theoretical knowledge of Support Vector Machine. There are many more applications which could be handled using SVM in various scenarios.

Hope this blog was helpful, good luck. Thank you.

And also if you required any technology you want to learn, let us know below we will publish them in our site http://tossolution.com/

Like our page in Facebook and follow us for New technical information.